数据挖掘与机器学习 线性回归设计 实训1

（1）实训目的

1.掌握回归的基本思想；

2.掌握梯度法的基本原理 。

（2）主要内容

1.实现一元线性回归；

2.画出散点图、回归参数与迭代次数的变化曲线；

3.分析不同数据变化对回归结果的影响。

（3）具体处理步骤

1. 导入数据集，绘制数据的散点图

data1.txt 数据集下载

1
2
3
4
5
6
7
8
9
import numpy as np
import matplotlib.pyplot as plt

data=np.loadtxt("data1.txt", delimiter=",") # 读取数据集，列索引分别是x和y

x=data[:,0:1] # 取x这列所有值,训练数据
y=data[:,1:]
plt.scatter(x,y) # 绘制散点图
plt.show()

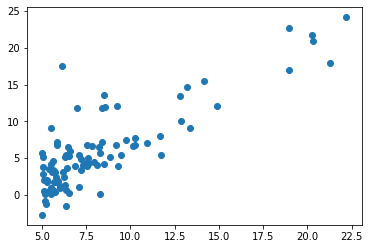
img-202304291223504

1
data.shape # 原数据集形状，n行m列
(97, 2)

2. 对特征进行归一化处理

1
2
3
4
5
def featureNormalize(x): # （特征值x的取值差别较大）需消除特征值的量纲
    avg = x.mean()
    sstd = np.std(x, axis=0, ddof=1) # 进行标准差标准化处理（ddof是分母为n-1,无偏估计）
    x = (x-avg)/sstd
    return x, avg, sstd

3.1 定义损失函数 h_theta是预测函数（假设函数），j_theta是损失函数

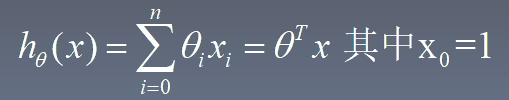
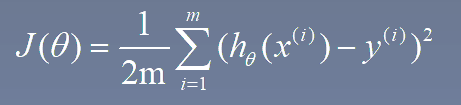
img-202304291221890 img-202304291221178 
1
2
3
def computeCost(x, y, theta): # 损失函数j_theta
    m = x.shape[0] # 获取第一维度的长度（行数），即X特征项对应的个数
    return np.sum((np.dot(x,theta) - y)**2)/(2*m)

3.2 梯度下降算法

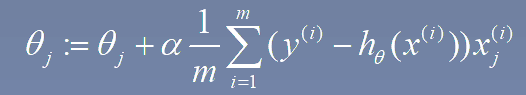
img-202304291222715
利用公式 theta : 是预测函数每项的系数，times：梯度下降次数，alpha：梯度下降参数变化率
1
2
3
4
5
6
7
8
9
10
11
def gradientDescent(x, y, theta, times, alpha):
    theta_0 = np.ones(x.shape[0]).T
    x = np.insert(x, 0, theta_0, axis=1) # 对原始数据加入一个全为1的列，方便后续计算
    m = x.shape[0] # 行数
    n = x.shape[1] # 列数
    costs = np.zeros(times) # 初始化损失数组
    for num in range(times): # 循环迭代，计算梯度下降的值
        for j in range(n):
            theta[j] = theta[j] + (alpha/m) * np.sum(y - np.dot(x,theta) * x[:,j].reshape(-1,1))
        costs[num] = computeCost(x, y, theta)
    return costs # 返回每次迭代计算的损失

4. 计算求得的直线

1
2
3
4
5
6
7
8
9
10
11
12
13
x_orgin=x # 分别取x，y这列的值
y_orgin=y

x1, avg, sstd = featureNormalize(x_orgin) # 得到经特征归一化后的特征值x

theta = np.zeros(x1.shape[1]+1).reshape(-1,1) # 变为1列的列向量（2个theta值）
times = 600
alpha = 0.01
costs = gradientDescent(x1, y_orgin, theta, times, alpha)

plt.scatter(x1, y_orgin) # x1是（-1~4）
h_theta = theta[0]+theta[1]*x1 # 预测的直线
plt.plot(x1, h_theta, color= 'red')

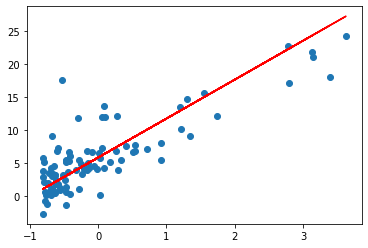
img-202304291224464

1
2
3
4
print('预测函数: y = %f + %f * x' % (theta[0], theta[1]))

# 验证，x=3时，y应该在23附近
print('x=3, y = %f' % (theta[0] + 3*theta[1]))
预测函数: y = 5.825092 + 5.884855 * x
x=3, y = 23.479657

5. 画损失函数，损失随迭代次数变化的曲线

1
2
x_times = np.linspace(1,times,times)
plt.plot(x_times, costs[0:times], color="orange",linewidth=3) # 纵坐标是损失值

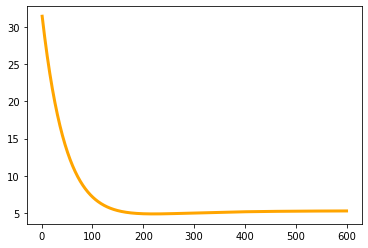
img-202304291224616

6. 结果分析

分析可知，当迭代次数到200次左右时，损失函数趋于收敛损失值达到最小值，迭代次数太多，可能使得出现过拟合现象

alpha 越小时，即步长越小，使得训练过程中的变化速度较慢，但可能更易于损失函数收敛

（4）参考资料

data1.txt 数据集下载

机器学习讲解-B站

使用梯度下降法求解线性回归问题

Python机器学习笔记 - AcWing